Ковариантность и контравариантность

Июль 25, 2014 Habibutsu

Содержание

• Введение
• Математика
• Теория категорий
• Программирование
• Java
• C#
• С++
• Scala
• Haskell
• Ссылки

Введение

Понятие инвариантна появилось в программировании сравнительно давно, благодаря использованию аксиоматической семантики в языках. Инвариант используется в теории верификации программ для доказательства правильности выпоплнения цикла либо для обозначения непротеворечивого состояния объекта в ОПП парадигме. С постепенным развитием компьютерной науки (Computer Science) она все больше начинает обогащаться терминами и определениями из смежных областей (математика, логика и др.). Ковариантность и контравариантность - можно считать одними из таких понятий, которые вошли в обиход сравнительно недавно и наверно наиболее популярными стали с появлением язка Scala где их реализация представленна особенно широко. В данной заметке в кратком виде приводятся определения данных терминов с точки зрения математики, теории категорий и программирования.

Математика

Определим три отображения для целых чисел:

• D : x → x + x (удвоение)
• N : x → 0 - x (отрицание)
• S : x → x * x (возведение в квадрат)

Рассмотрим отношение порядка в двух различных пространствах:

• x ≤ y
• F(x) ≤ F(y)

Будет ли оно выполняться при переходе от одного пространства к другому?

Удвоение

• (x ≤ y) = (D(x) ≤ D(y)) - выполняется

Пример: 2 ≤ 3 = (D(2) ≤ D(3)) = 4 ≤ 6
Отношение порядка выполняется - вариантность

Отрицание:

• (x ≤ y) = (N(x) ≤ N(y)) - не выполняется
• (x ≤ y) = (N(y) ≤ N(x)) - выполняется

Пример: 2 ≤ 3 ≠ (N(2) ≤ N(3)) = -2 ≤ -3, однако 2 ≤ 3 = (N(3) ≤ N(2)) = -3 ≤ -2
Отношение порядка меняется на потивоположное - контравариантность

Возведение в квадрат:

• (x ≤ y) = (S(x) ≤ S(y)) - не выполняется
• (x ≤ y) = (S(y) ≤ S(x)) - не выполняется

Пример: -3 ≤ -2 ≠ (S(-3) ≤ S(-2)) = 6 ≤ 4, и 2 ≤ 3 ≠ (S(3) ≤ S(2)) = 6 ≤ 4
Отношение порядка не выполняется в обоих случаях- инвариантность

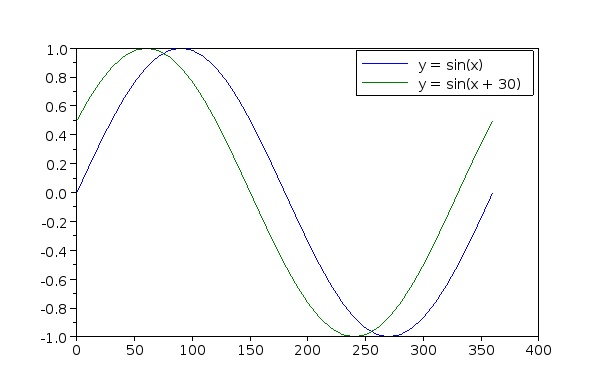
В качестве еще одного примера рассмотрим функцию f: x → sin(x)
Если систему координат сдвинуть на +a по оси X, то график функции сместится в противоположном направлении на -a т.е. при смене базиса (системы координат) компоненты изменяются с помощью преобразования обратного преобразованию базиса - функция является контравариантной относительно оси X. В то же время если сдвинуть систему координат по оси Y а +a, то график функции сместится в том же направленннии - функция является ковариантной относительно оси Y.

Теория категорий

Взаимосвязь между теорией категорий и теорией типов можно выразить следующим образом [1]:

• Объект - Тип данных
• Морфизм - Программа

В качестве стандартного примера рассмотрим функтор степени множеств: P: Set → Set [7].

Ковариантный функтор степени P: Set → Set ставит в соответсвие каждому множеству A его множество-степень P(A), а каждой функии f: A → B - отоброжение P(f): P(A) → P(B), переводящий любое подмножетсво X ⊆ A в его образ f(X) ⊆ B.

Если f: a → a * a, тогда множество A = [1, 2] посредством f: A → B будет отображено в B = [1, 4], при этом PA = [[], [1], [2], [1, 2]] в случае если Pf = f: a → a * a будет отображено в PB = [[], [1], [4], [1, 4]]

Контравариантный функтор степени P: Set → Set ставит в соответсвие каждому множеству A его множество-степень P(A), а каждой функии f: A → B - отоброжение P(f): P(B) → P(A), переводящий любое подмножетсво X ⊆ B в его образ f^-1(X) ⊆ A.

Если f: a → a * a, тогда множество A = [1, 2] посредством f: A → B будет отображено в B = [1, 4], при этом PB = [[], [1], [4], [1, 4]] в случае если Pf = f^-1: a → a * a будет отображено в PA = [[], [1], [2], [1, 2]]

Программирование

Для возможности рассуждать об отношении порядка между типами (тип/подтип) необходимо какое-то формальное правило. Такое правило было предложено Барбарой Лисков в 1987 году на конференции в основном докладе под названием "Абстракция данных и иерархия" [7].

Другими словами, если некоторый тип S можно подставить везде, где используется тип Т и поведение программы не будет меняться, то тип T является базовым по отношению к S при этом подразумевается, что тип S поддерживает все те же операции что и тип T и при этом все операции типа S требуют меньшего, а предоставляют большее чем соответсвующие операции в T.

Исходя из этого определения можно дать понятия ко-/контр-вариантных типов

• Ковариантность - случай когда более конкретный тип S может быть подставлен вместо более обобщенного типа Т
• Контрвариантность - случай когда более общий тип Т может быть подставлен вместо более конкретного типа S
• Инвариантность - случай когда подставлять можно только определенный тип

При ковариантности иерархия наследования сохраняется в прямом направлении, при контравариантности она меняется на противоположное, а при инвариантности не определена.

Обычно ковариантность и контравариантность смешиваются в одном типе, например для типа произвольной функции которая является контравариантной по своим входным аргументам и ковариантной по своим выходным аргументам т.к. аргументы это нечто что требуется в то время как результат это нечто что предоставляется.

Еще одним важным следствием из вышеприведенных определений является то, что ковариантность типо-безопасна для операций чтения, а контравариантность для операций записи.

Чтобы все это уяснить, лучше обратиться к реальным примерам.

Java

Возьмем следующую иерархию типов:

class A {}

class B extends A{}

class C extends B {}

class D extends C {}

Т.к. массивы в Java решено было сделать ковариантными, то вместе с отношением тип B является подтипом A, вводится отношение тип Array<B> является подтипом Array<A>. Такой подход был обусловлен желанием разработчиков Java предоставить возможность реализовывать обобщенные функции (когда обобщенных типов еще не было в языке) в которые можно передавать произвольный ссылочный тип.

public class TestArray {
    public static void main(String[] args){
        String[] strArray = new String[] {"string1", "string2", "string3"};
        print(strArray);
    }

    public static void print(Object[] objectArray){
        for (Object v : objectArray)
            System.out.print(v + "\n");
    }
}

$ javac TestArray.java 
$ java TestArray 
string1
string2
string3

Однако это приводит к тому, что допускается не типо-безопасное присваивание и соответсвенно некорректное поведение на runtime (вспомните, что ковариантность типо-безопасна для операций чтения, а не записи):

public class TestArray {
    public static void main(String[] args){
        String[] strArray = new String[] {"string1", "string2", "string3"};
        Object[] objectArray;
        objectArray = strArray;
        objectArray[2] = 123;
    }
}

$ javac TestArray.java 
$ java TestArray 
Exception in thread "main" java.lang.ArrayStoreException: java.lang.Integer
    at TestArray.main(TestArray.java:6)

С появлением обощенных типов (generics), которые по умолчанию инвариантны необходимость в таком подходе отпала, но для обратной совместимости поведение было сохранено.

Иногда, все-же, для увеличения гибкости есть необходимоть сделать коллекции ковариантными/контравариантными. Java предоставляет такую возможность посредством специального вида типа с параметрами, называемого ограниченным типом групповых символов (wildcard-тип).

Ковариантность

Для объявления коллекции ковариантной можно использовать констркуцию ? extends, однако в этом случае будут доступны только операции чтения, а при попытке вызова не типо-безопасных операций записи возникнет ошибка при компиляции. Например нельзя добавить елементы типа B т.к. коллекция может ссылаться на любой из подтипов типа А.

ArrayList<? extends A> arrayA_covariant;
arrayA_covariant = arrayA;
arrayA_covariant = arrayB;
arrayA_covariant = arrayC;
arrayA_covariant = arrayD;

A varA = arrayA_covariant.get(0);

/*      
//error: no suitable method found
arrayA_covariant.add(new B());
arrayA_covariant.add(new C());
*/

В результате можно реализовать какую-то обобщенную функцию не изменющую исходную коллекию (например вывод на экран всех елементов) для типа А, и использовать ее для елементов являющимися подтипами А (B, C или D).

Контравариантность

Для объявления коллекции контравариантной можно использовать констркуцию ? super, однако теперь будут доступны только операции записи, а при попытке вызова операций чтения возникнет ошибка при компиляции.

ArrayList<? super C> arrayC_contravariant;

arrayC_contravariant = arrayA;
arrayC_contravariant = arrayB;
arrayC_contravariant = arrayC;
// error: incompatible types:
// arrayC_contravariant = arrayD;


arrayC_contravariant.add(new C());
arrayC_contravariant.add(new D());

/*
// error: incompatible types
A varA = arrayC_contravariant.get(0);
B varB = arrayC_contravariant.get(0);
C varC = arrayC_contravariant.get(0);
D varD = arrayC_contravariant.get(0);
*/

Механизм объявления ко/контравариатных отношений в Java иногда еще назвают PECS (producer-extends, consumer-super). Тип предоставляющий данные (которые будут читаться) объявляется при помощи <? extends T>, а тип предназначенный для потребителя (который необходимо наполнить) объявляется при помощи <? super T>

В качестве реального примера можно рассмотреть упрощенную реализацию стека.

class Stack<T> {
    private T[] elementData;

    private int elementCount = 0;

    private void ensureCapacityHelper(int minCapacity){
        if (minCapacity - elementData.length > 0)
            elementData = Arrays.copyOf(elementData, 2 * elementData.length);
    }
    public Stack(){
        this(10);
    }

    @SuppressWarnings("unchecked")
    public Stack(int initialCapacity){
        elementData = (T[]) new Object[initialCapacity];
    }

    public T push(T item){
        ensureCapacityHelper(elementCount + 1);
        elementData[elementCount++] = item;
        return item;
    }

    public T pop(){
        T item;
        if (elementCount == 0)
            throw new EmptyStackException();
        item = elementData[elementCount - 1];
        elementCount--;
        elementData[elementCount] = null;
        return item;
    }
    /*
    * Добавляем елементы из коллекции в стек.
    * В качестве входного параметра можно передавать коллекции
    * производных от T типов.
    */
    public void pushAll(Collection<? extends T> c) {
        for(T item: c)
            push(item);
    }
    /*
    * Извлекаем елементы из стека в коллекцию.
    * В качестве входного параметра можно передавать коллекции
    * супертипов для Т.
    */
    public void popAll(Collection<? super T> c) {
        while(elementCount > 0)
            c.add(pop());
    }
}

Пример использования:

// Ковариантность
Stack<A> stackA = new Stack<A>();
ArrayList<B> arrayB = new ArrayList<B>();
stackA.pushAll(arrayB);

// Контравариантность
Stack<C> stackC = new Stack<C>();
ArrayList<A> arrayA = new ArrayList<A>();
stackC.popAll(arrayA);

Ковариантность/контравариантность также свойственна для иерархии наследования.

Ковариантность:

class Super {
    A getSomething(){}
}
class Sub extends Super {
    B getSomething() {}
}

Контрвариантность:

class Super{
    void doSomething(B parameter)
}
class Sub extends Super{
    void doSomething(A parameter)
}

Как видно из примеров ковариантность свойственна выходным параметрам, а контравариантность - входным.

C#

В C# нет аналога wildcard типов из Java, однако с версии Visual C# 2010 ковариантность/контравариантность была добавлена в обобщенных интерфейсах и типах делегатов. Интерфейс IEnumerable является ковариантным, а например IComparer контравариантным. [11]

Пример того как можно определить ковариантный/контравариантный интерфейсы:

public interface ICovariant <out T>{
    T Get();
}

public interface IContravariant <in T> {
    void Add (T item);
}

Пример реализации стека на C#, аналогичный приведенному выше для Java:

public class Stack<T>
{
    private T[] elementData;
    private int elementCount = 0;

    private void ensureCapacityHelper(int minCapacity){
        if (minCapacity - elementData.Length > 0)
            Array.Resize(ref elementData, elementData.Length * 2);
    }

    public Stack(int initialCapacity){
        elementData = new T[initialCapacity];
    }

    public Stack(): this(10){
    }

    public T Push(T item){
        ensureCapacityHelper(elementCount + 1);
        elementData[elementCount++] = item;
        return item;
    }

    public T Pop(){
        if (elementCount == 0)
            throw new InvalidOperationException ();
        T item = elementData[elementCount - 1];
        elementCount--;
        elementData[elementCount] = default(T);
        return item;
    }

    public void pushAll (IEnumerable <T> enumerable)
    {
        foreach (T t in enumerable)
        {
            Push(t);
        }
    }

    public void ForEach (Action <T> action)
    {
        if (action == null)
            throw new ArgumentNullException ("action");

        while(elementCount > 0)
            action(Pop());
    }
}

Из-за того что в C# ковариантными являются только некоторые интерфейсы и делегаты полностью воспроизвести поведение для метода popAll как в Java не получится, но можно реализовать ForEach который достанет все елементы и передаст их в делегат action. Использоваться может так:

// Ковариантность
List<B> listB = new List<B>();

Stack<A> stackA = new Stack<A>();
stackA.pushAll(listB);

// Контравариантность
List<A> listA = new List<A>();
Stack<C> stackC = new Stack<C>();
Action<A> PopTolistA = (Item) => { listA.Add(Item); };
// PopTolistA предназначен для объектов типа А, но передаем как
// делегат для объектов типа C
stackC.ForEach(PopTolistA);

C++

В C++ нет обобщенных типов и как следствие параметрического полиморфизма (шаблонные типы представляют собой просто кодогенерацию). Основной вид полиморфизма - полиморфизм наследования.

Ковариантность

class A {};
class B : public A {};
class C : public B {};

class Super {
    public:
        virtual B *get_something() { return new B(); }
};

class Sub : public Super {
    public:
        // должны были вернуть елемента типа C, но вернули A
        virtual A *get_something() { return new A(); }
};

int main(){
    return 0;
}

$ g++ -W -Wall -ansi -pedantic -c covariance.cpp
covariance.cpp:12:20: error: invalid covariant return type for ‘virtual A* Sub::get_something()’
covariance.cpp:7:20: error:   overriding ‘virtual B* Super::get_something()’

Контравариантность

class A {};
class B : public A {};
class C : public B {};

class Super {
    public:
        virtual void do_something(B &b) { }
};

class Sub : public Super {
    public:
        // должен быть A, но сделали C
        virtual void do_something(C &c) { }
};

int main(){
    B b;
    C c;
    Sub sup_item;
  
    sup_item.do_something(b);
    sup_item.do_something(c);
    return 0;
}

$ g++ -W -Wall -ansi -pedantic -c contravariance.cpp
contravariance.cpp: In function ‘int main()’:
contravariance.cpp:20:28: error: no matching function for call to ‘Sub::do_something(B&)’
contravariance.cpp:20:28: note: candidate is:
contravariance.cpp:12:22: note: virtual void Sub::do_something(C&)
contravariance.cpp:12:22: note:   no known conversion for argument 1 from ‘B’ to ‘C&’

Scala

Scala обладает гораздо более широкой системой типов по сравнению с Java или C#. Для возможности определения отношений между типами в язык введены аннотации вариативности (variance annottions), которые задаются при помощи префиксов перед типовыми переменными: "+" в случае ковариантного типа либо "-" для контравариантного.

Для проверки корректности аннотаций вариативности, компилятор классифицирует все позиции в теле класса или примеси на положительные, отрицательные или нейтральные. Типовой параметр аннотированный "+" может быть использован только в положительной позиции тогда как аннотированный при помощи "-" только в отрицательной. Типовые параметры без аннотации могут использоваться в любой позиции [12]

Определение функции с одним аргументом выглядит следующим образом:

trait Function1[-T, +R] extends AnyRef {

    def apply(arg1: T): R

}

Компилятор строго отслеживает в какой позиции находятся параметры и не допускает их неправильного использования. Тем не менее для большей гибкости иногда возникает необходимость обойти эти ограничения. Для этого в язык введено понятие ограничивающего полиморфизма - F-bounded polymorphism [13]. Определение класса для реализации стека (аналогичному приведенному выше) с использованием различных вариантов может выглядеть следующим образом:

abstract class AbstractStackCovariant[+T]{
    def pop(): T
    
    def push[U >: T](item: U)

    def popAll[U >: T](collection: Array[U])

    def pushAll[U >: T](collection: Iterable[U])
}

abstract class AbstractStackContravariant[-T]{
    def pop[U <: T](): U
    
    def push(item: T)

    def popAll[U <: T](collection: Array[U])

    def pushAll[U <: T](collection: Iterable[U])
}

abstract class AbstractStackInvariant[T]{
    def pop(): T
    
    def push(item: T)

    def popAll[U >: T](collection: Array[U])

    def pushAll[U <: T](collection: Iterable[U])
}

Haskell

В Haskell нет изменяемых значений, поэтому все типы ковариантны. В то же время в языке активно используется понятие функтора, который, как было показано выше (см. Теория категорий), может быть как ковариантным так и контравариантным. Само поянтие, как и монаидальные типы для работы с которыми он предназначен, было позаимствовано из теории категорий.

Пример ковариантного фуктора, имеющегося в стандартной библиотеке:

class Functor f where
    fmap :: (a -> b) -> f a -> f b

Определение контравариантного функтора тривиальна:

class ContrFunctor f where
    contrmap :: (a -> b) -> f b -> f a

В качестве примера можно рассмотреть вариант использования contrmap принимающую функцию, которая вычисляет длину списка, для вычисления длины множества.

newtype ContrFun a b = ContrFun ( b -> a )

instance ContrFunctor (ContrFun cf) where
    contrmap f ( ContrFun cf ) = ContrFun ( cf . f)

listLengther :: ContrFun Int [a]
listLengther = ContrFun Prelude.length

setLengther :: ContrFun Int (Set a)
setLengther = contrmap Set.toList listLengther

calculate :: ContrFun a b -> b -> a
calculate (ContrFun f) a = f a

test_listLengther = 4 == calculate listLengther [1, 2, 3, 4]

test_setLengther = 4 == calculate setLengther (Set.fromList [1, 2, 2, 3, 4, 4])

Определения контравариантного функтора в стандартной библиотеке нет, но на http://hackage.haskell.org можно найти готовый пакет [15].

Дополнение

Используемые версии компиляторов:

Ссылки

• [1] General theory of natural equivalences.
• [2] Physics, Topology, Logic and Computation: A Rosetta Stone (John C. Baez, Mike Stay)
• [3] Физика, топология, логика и теория вычислений: Розеттский камень (Дж. К. Баез, М. Стэй) - Перевод Р. Душкин
• [4] Category Theory - Wikipedia, the free encyclopedia
• [5] Category Theory - Stanford Encyclopedia of Philosophy
• [6] Теория типов — Википедия
• [7] Топосы. Категорный анализ логики - Голдблатт Р., 1983 г.
• [8] Категории для работающего математика - Сандерс Маклейн, 2004 г.
• [9] Data abstraction and hierarchy - Liskov, Barbara
• [10] Covariance and contravariance (computer science) - Wikipedia
• [11] Covariance and Contravariance (C# and Visual Basic)
• [12] Programming in Scala, 2nd ed
• [13] F-Bounded Polymorphism for Object Oriented Programming - Peter Canming, William Cook and other
• [14] 24 Days of Hackage: contravariant
• [15] The contravariant package